URL: LeetCode Problem
Problem Description
You are given an m x n integer matrix matrix with the following two properties:
Each row is sorted in non-decreasing order. The first integer of each row is greater than the last integer of the previous row. Given an integer target, return true if target is in matrix or false otherwise.
You must write a solution in O(log(m * n)) time complexity.
Examples:
- Example 1:
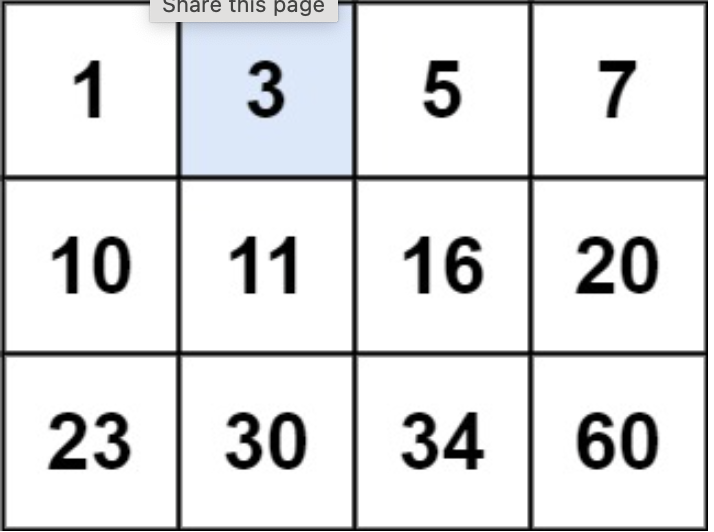
Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
Output: true
- Example 2:
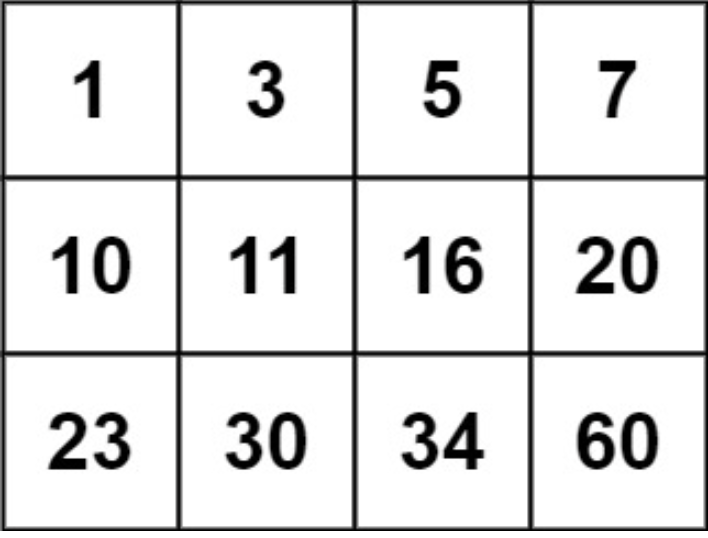
Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
Output: false
Constraints:
- m == matrix.length
- n == matrix[i].length
- 1 <= m, n <= 100
- 104 <= matrix[i][j], target <= 104
Answer
Intuition
To achieve O(log(m * n)) time complexity, we can apply binary search twice: first to identify the row that might contain the target, and then to find the target within that row.
Complexity
Time complexity: O(log(m*n))
Space complexity: O(1)
- Use only a constant amount of space to store our variables (left, right, midCol, midRow, top, bottom, cols, rows),
Code
class Solution:
def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
top, bottom = 0, len(matrix)-1
cols = len(matrix[0])
rows = len(matrix)
# Check the row
while top <= bottom:
midRow = (bottom-top)//2 + top
# Check the column
row = matrix[midRow]
left, right = 0, len(row)-1
while left <= right:
midCol = (right - left) // 2 + left
if row[midCol] == target:
return True
# target is higher than the selected number
if row[midCol] < target:
left = midCol + 1
# target is lower than the selected number
if row[midCol] > target:
right = midCol - 1
if matrix[midRow][0] < target:
top = midRow + 1
if matrix[midRow][0] > target:
bottom = midRow - 1
return False
